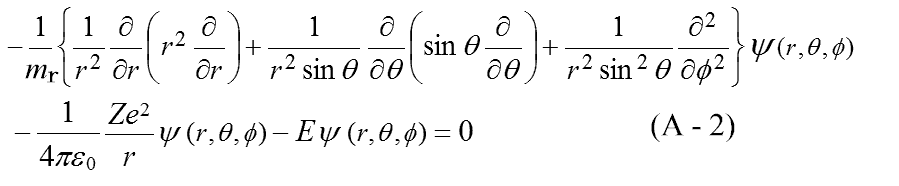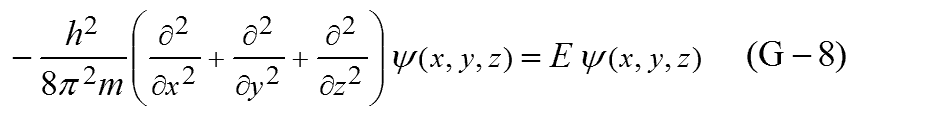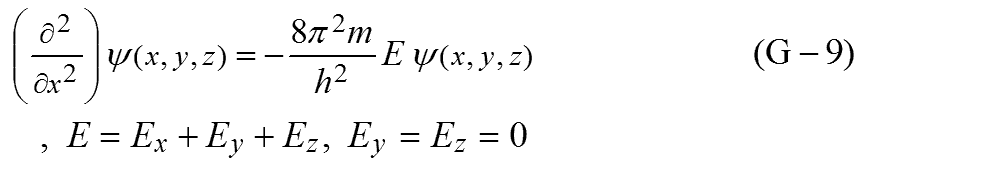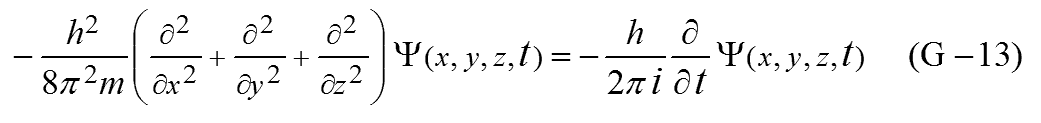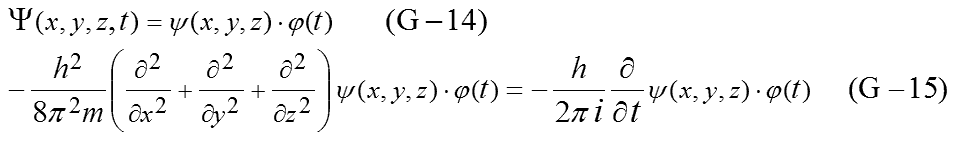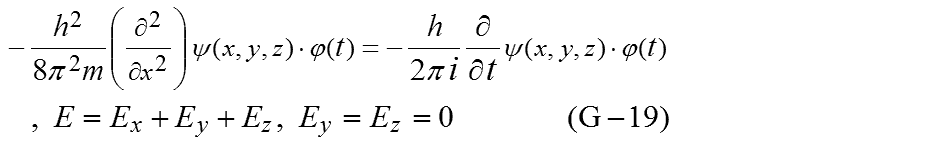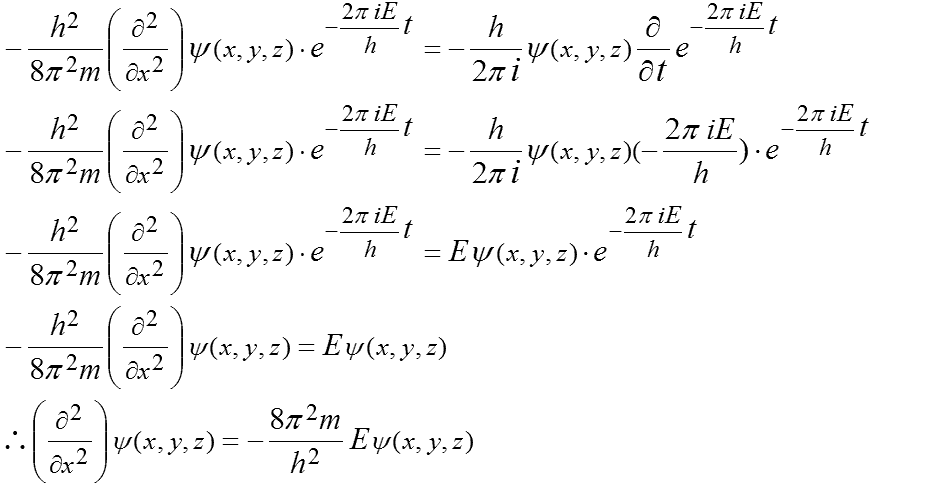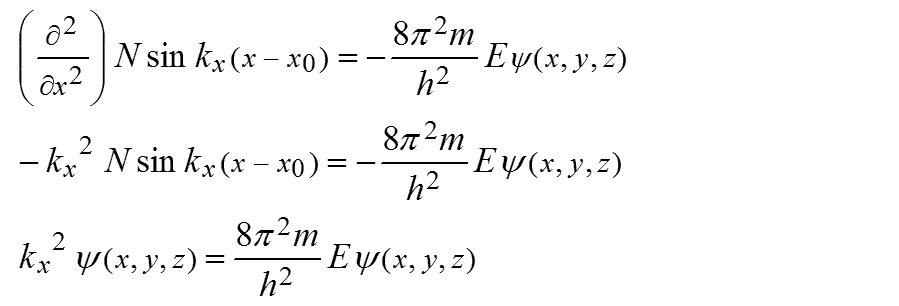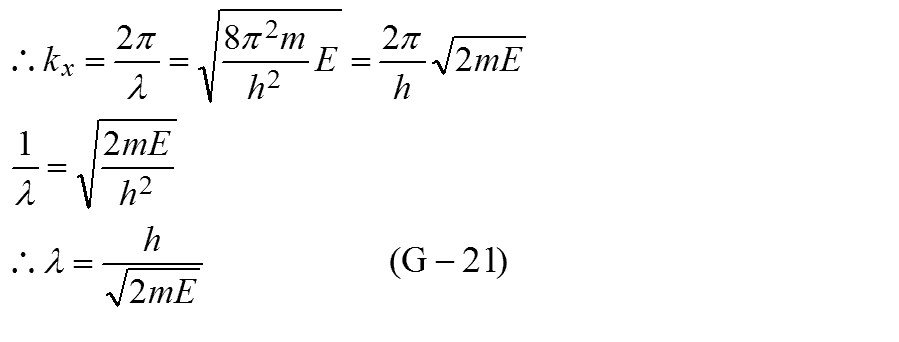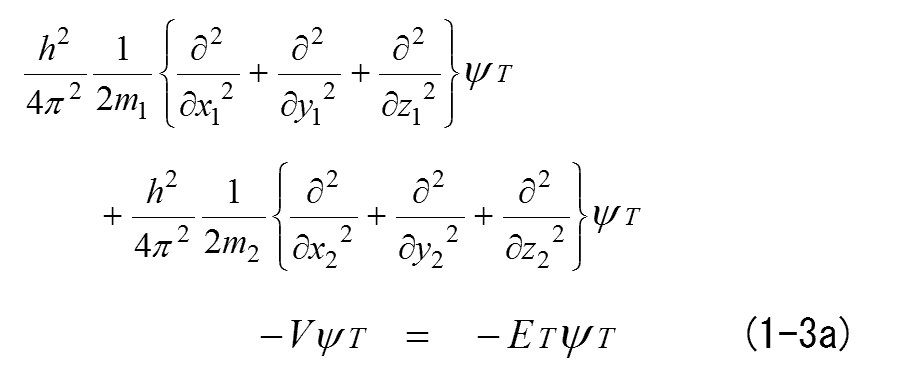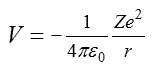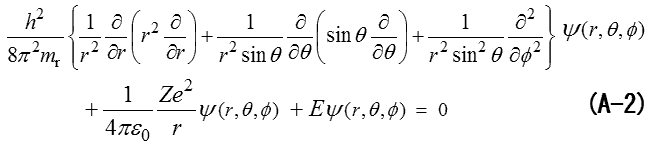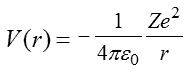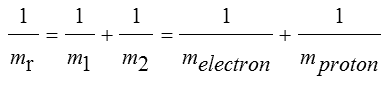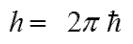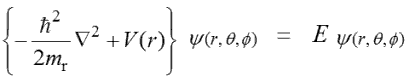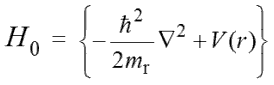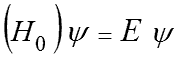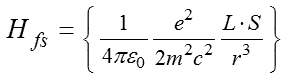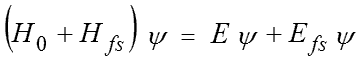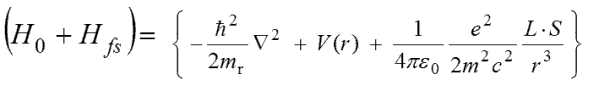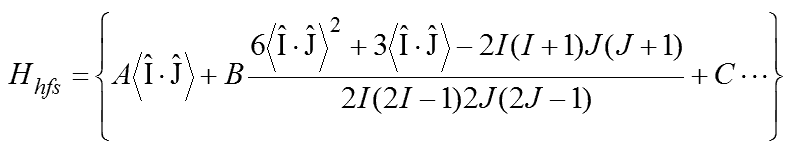水素原子の「電子軌道」の波動関数,シュレディンガー方程式の解
G.エネルギー準位・原子スペクトル・並進運動・Zeeman Effect
エネルギー準位
エネルギー式を求めます。
再掲

式(E-6)と式(E-12)より次のようになります。

中辺と右辺を2乗します。
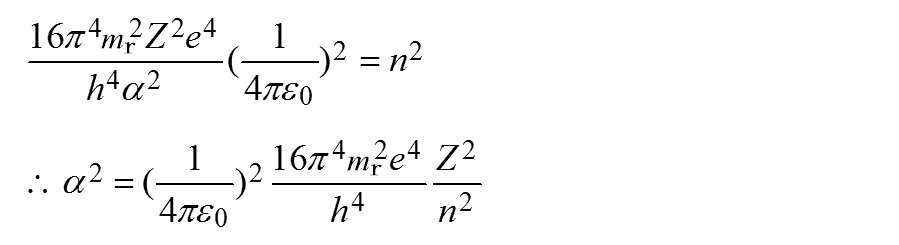
これに式(E-5)を代入すると次のようになります。
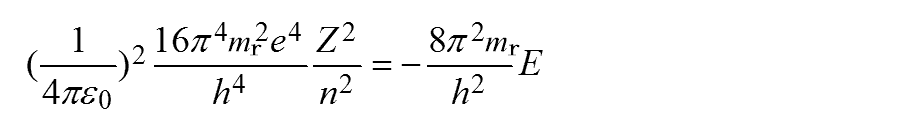
Eは、次のように得られます。
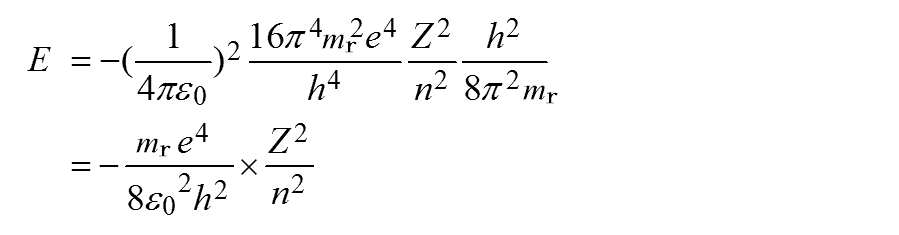
これは主量子数nで決まる値であり、主量子数nのエネルギー準位Enは次のように得られます。
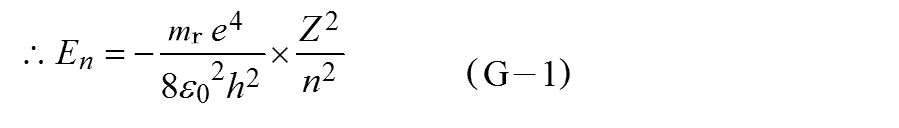
原子スペクトル
最初に、原子スペクトルの歴史をたどってみます。1817年、W. Wollaston(英)そしてJ. Fraunhofer(独)が、太陽光のスペクトルに暗線を見出しフラウンホーファー線と名付けられました。1860年にG. Kirchhoffが元素に由来する原子スペクトルであることを発見しました。そしてR. Bunsenとともに原子スペクトルによる元素同定の道を開きました。
1885年、J. J. Balmerが水素原子のバルマー系列で次のような式を見出し、今で言う量子数で表わされることを発見しました。量子力学の幕開けです。

そして1890年、J. Rydbergは次のような式を完成させました。
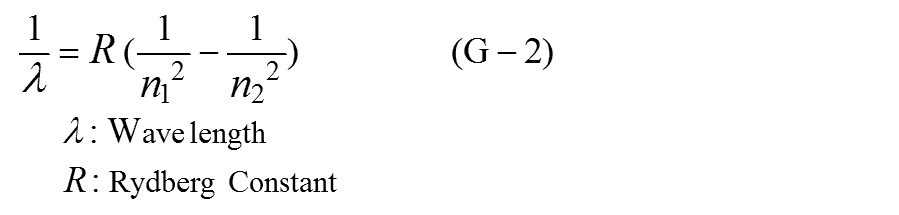
1900年、M. Plankは、「エネルギー差⊿Eが、電磁波の振動数νまたは波長λを使い、次式で表わせる。」ことを発表しました。

20世紀初頭、式(G-2)に一致するライマン系列(1914年)、パッシェン系列(1908年)、さらにはブラケット系列(1922年)も確認され、量子数という概念は確実なものとなりました。残念ながら創始者のJ. J. Balmerはこれらの成果を見ることなく19世紀末に亡くなり、自らノーベル賞を受賞することはありませんでした。
波数表示のエネルギー1/λ
再掲

エネルギー準位差は次のようになります。
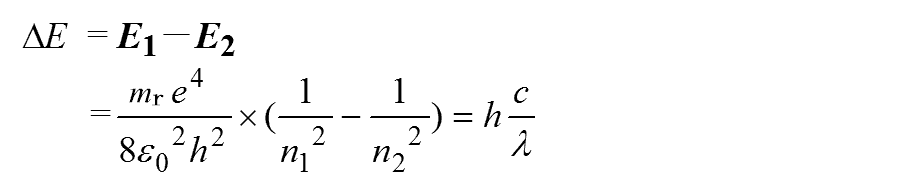
波数1/λは次のようになります。
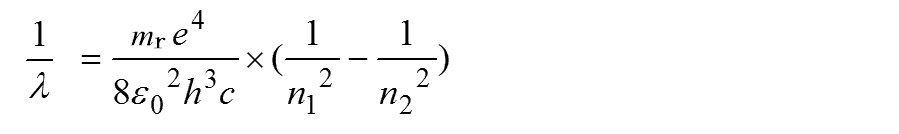
波長の逆数がエネルギーなるのは?と思いますが。上式見れば分かるように、「波数表示のエネルギー1/λ」にプランク定数hと光速cを掛けたものが正式なエネルギーになります。慣例的にhとcが省略されています。
再掲

リュードベリー定数Rは次のようになります。

定数の数値を代入すると次の値になります。
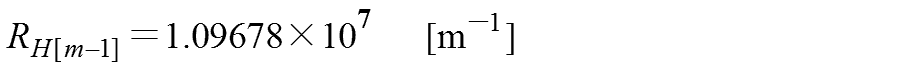
原子スペクトルで使用するセンチメートル当りの波数1/λは、単純に1/100で次のようになります。
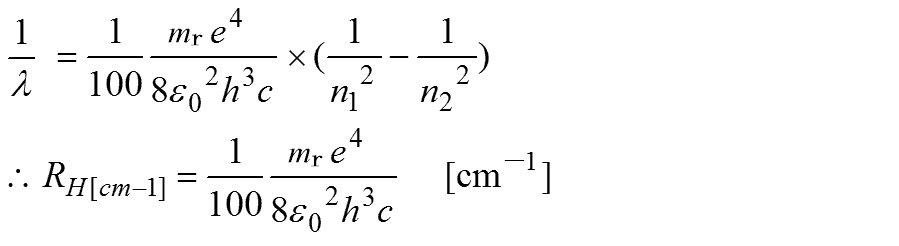
[cm-1]単位のリュードベリー定数は次のようになります。

計算したエネルギー準位を下表に示しました。また表中には原子スペクトル測定値も対比させています。

計算値と測定値の差は1カイザー弱であり、0.001%前後の誤差しかない。
水素原子の「厳密解」と言われる1つの理由になっています。
「厳密解」と言われるもう1つの理由は、唯一水素原子だけが全く近似を使うことなく「シュレディンガーの波動方程式」を解けるからです。
水素原子の原子スペクトル
水素原子は、主量子数nだけでエネルギー準位が決まります。原子スペクトルの振動数νは、エネルギー準位の差⊿E=hνで決まります(hはプランク定数)。エネルギー準位と原子スペクトル系列は次のエネルギー準位図のようになります。

微細構造、超微細構造、ゼーマン効果(Zeeman Effect)
水素原子には、主量子数n以外に、微細構造、超微細構造と呼ばれるエネルギー準位の分裂があるようです。
微細構造(Fine Structure)
微細構造を含む水素原子のエネルギー準位図です。
図中左下から、
n=1:0 [cm-1]、
n=2:82,259.158 [cm-1]、
n=3:97,492.304 [cm-1]、
n=4:102,823.90 [cm-1]
のように、エネルギー準位は主量子数nによってほぼ決まります。
各エネルギー準位差を左のDifferenceで見ていくと、
n=1と2の差は 82,259.0 [cm-1]、
n=2と3の差は 15,233.0 [cm-1]、
n=3と4の差は 5,331.0 [cm-1]と、
約80,000~5,000 [cm-1]の大きな値です。
ここまでは電子スピンが無い場合の各主量子数nのエネルギー準位です。
実際には電子スピンは常にあるので、この準位は無いのですが。最初期の量子力学では低分解能スペクトルしか無かったので、これで議論していました。しかしスペクトルの分解能が上がるにつれ、各主量子数nのピークには複数のピークが混在していることが発見されました。これが微細構造(Fine Structure)です。
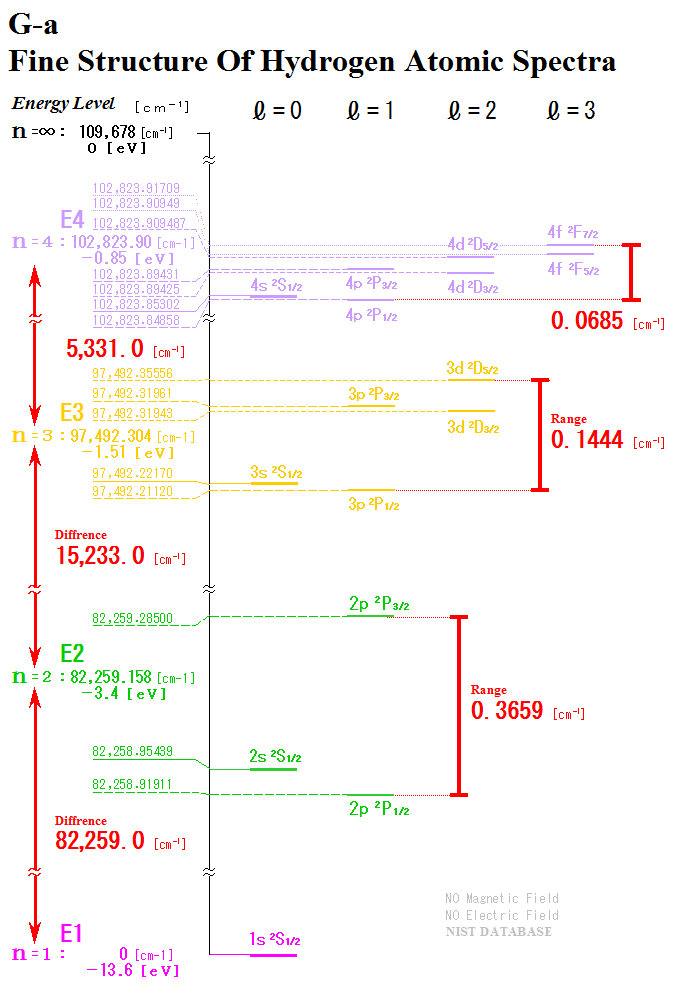
各主量子数nの中の微細構造のエネルギー準位差を右端のRangeで示しています。0.3659~0.0685[cm-1]と大変小さい値です。微細構造は、電子スピンと軌道磁気モーメントのCombinationの違いによって生じる、異なるエネルギー準位です。
電子スピンと軌道磁気モーメントの相互作用(カップリング)により、
高エネルギー状態の
2P 2P3/2と、
低エネルギー状態の
2P 2P1/2
に分裂します。つまり主量子数n=2でほぼ決まるエネルギー準位には、0.3659 [cm-1]と大変小さな差異ですが、3個の異なるエネルギー準位がある。これが微細構造です。
1920年ころから発見され始めました。微細構造は、ハミルトニアンHに、新たに相対論補正項、電子スピン補正項を追加することにより議論されます。
また
2S 2S1/2と
2P 2P1/2は、エネルギー準位差が0.035 [cm-1]と一桁小さいため、発見されたのは1940年代でした。この差がラムシフト(Lamb Shift)です。
※ 左下n=1が水素原子の基底状態で原子スペクトルでは0[cm-1]基準としています。慣例的にこちらを使います。一方、-13.6eVの絶対値が水素原子のイオン化エネルギーです。基底状態の水素原子の電子を、無限遠まで引き離すのに必要なエネルギーです。無限遠が基準0eVで、エネルギー値はマイナスeVです。こちらが正式なエネルギー準位ですが、[cm-1]表示との換算は容易です。
超微細構造(Hyperfine Structure)
微細構造は「電子スピンとのカップリング分裂」でした。超微細構造(Hyperfine Structure)は「さらに核スピンとのカップリング分裂」です。下図、縦軸はエネルギー準位です。右から2番目の列にHyperfine Structureを示しています。
水素の核スピンは1/2であるため、
Fine Structureの各エネルギー準位は
それぞれ2個に分裂します。
Hyperfine Structureは、Fine Structureより更に1桁~2桁小さなカップリング分裂(エネルギー準位差)です。高分解能の原子スペクトル装置でも、やっと測定できるか、できないというレベルです。

前図中の左上からもう少し見てみると、
Balmer Model: 1886年にJ.J.Balmerは、主量子数nだけで電子軌道を分類しました。n=1はK殻(1s)、n=2はL殻(2sと2p)、n=3はM殻(3sと3pと3d)です。当時の超低分解能装置では殻の中は識別できませんでした。
Bohr Model: 1913年にN.Bohrは、「同じ殻の中にs軌道p軌道d軌道などの異なる電子軌道がある。遠心力と静電引力がつり合っている。電子が原子核を中心とした円軌道を公転している。」というBohrモデルを発表しました。ただ当時の低分解能の原子スペクトル装置では図中に示すOld3s、Old3p、Old3dを誤識別していたようで残念ですが、Bohrモデルの理論は、球そしてエネルギー状態方程式へと姿を変えましたが、シュレディンガー方程式の根幹を成しています。N.Bohrは1922年ノーベル賞を受賞しました。
■Bohrモデル■
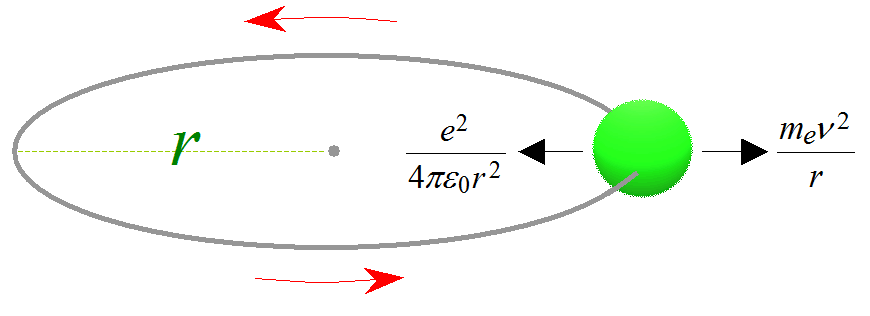
接線速度vで等速円運動する質量meの電子は、遠心力mev2/rがある。一方、電荷-eの電子は、電荷+eの核よりe2/(4πε0r2)の静電クーロン引力を受ける。この遠心力と静電クーロン力はつり合って、次式となる。

Bohrモデルはベクトルで表すことが可能です。円運動をして元の箇所に戻ります。しかし円周長は波長λの整数倍でなければなりません。電子運動のベクトルの「方向」と「速度」を予測可能で運動方程式で表せます。軌跡も追跡できます。
私はこの理論が好きです。Schrodingerも量子化・エネルギー状態方程式に変換してSchrodinger Equationに採用しています。しかし現実の今日は、最初のモデルの話にふれると、瞬殺するのではないかと。
あまり良くない例で混乱するかもしれませんが、現実の取引は、物々交換から現金決済主流へと変わってきました。そして各国の現金の相対価値は外国為替で流動的に決まります。
量子力学でも、最初のモデルであるBohrモデルはニュートン力学+電磁気学を基礎とする2次元の円運動ですが、これに1923年にW.K.Heisenbergが発表した「不確定性原理」が追加されて3次元の球面へと変わります。そして「不確定性原理」により、ベクトルが使えなくなります。
■「なんでベクトルは使えない?」■
ここでは「不確定性原理」の詳細は述べませんが、ベクトルの「方向」と「大きさ」の予測が不可となります。ただし瞬間、瞬間は、宇宙遊泳している電子にも個々のベクトルがあります。ベクトルはランダムに次々と変化するため予測が不可ですが、個々のペクトルは連続的に繋がり永遠に回ります。
■量子化モデル■
Heisenbergの「不確定性原理」により、ベクトルで表すことが不可能となりました。ゆえに量子化モデルであるSchrodinger Equationは、静電ポテンシャルエネルギーと運動エネルギーから構成されるエネルギー状態方程式です。これは1926年にE.Schrodingerが発表しました。
Bohrモデルでの2次元の円運動は、「不確定性原理」により、3次元の球になります。遠心力と静電クーロン力は、依然として吊り合っているので、Bohr半径の球面が考えられます。半径方向の「不確定性原理」も加味されるので、電子はBohr半径付近の球殻に最大確率密度があります。電子は、この球殻付近を連続的に移動しています。しかし「不確定性原理」によりベクトルの「方向」と「大きさ」は常に変化していて予測が不可能です。表現方法は、2タイムラグある移動平均ですが、軌跡では表せないので一般には電子の存在確率をdot散布図で表します。
水素原子は陽子1個の周囲に電子1個が存在します。この唯一の電子が、ボーア半径の球殻付近を飛び回ります。
ボーア半径を大幅に逸脱する確率は大変小さい。ましてや無限遠方へと逃亡してイオン化する確率は0に等しい。原子核に電子が捕獲されるのは、放射性同位元素以外は確認されていません。これは原子核近傍では反発力が存在するためです。ただ今回の式は、この反発力を式中に考慮していないので、原子核近傍については議論できません。
ゼーマン効果(Zeeman Effect)
エネルギー準位の分裂
上図右端オレンジ色で示しているのが、微弱磁場下でのエネルギー準位です。エネルギー準位差が、超微細構造より更に小さいことがわかります。
しかし強磁場下では、次図に示すように、突然、
High Energy Levelと
Low Energy Levelに
激しく分裂し、2つのエネルギー準位に非常に大きな落差が現れます。
この落差は、外部磁場をより強くすれば、更にどんどん大きくなります。これが、「Zeeman Shock」または「Zeeman Sift」と呼ばれるものです。
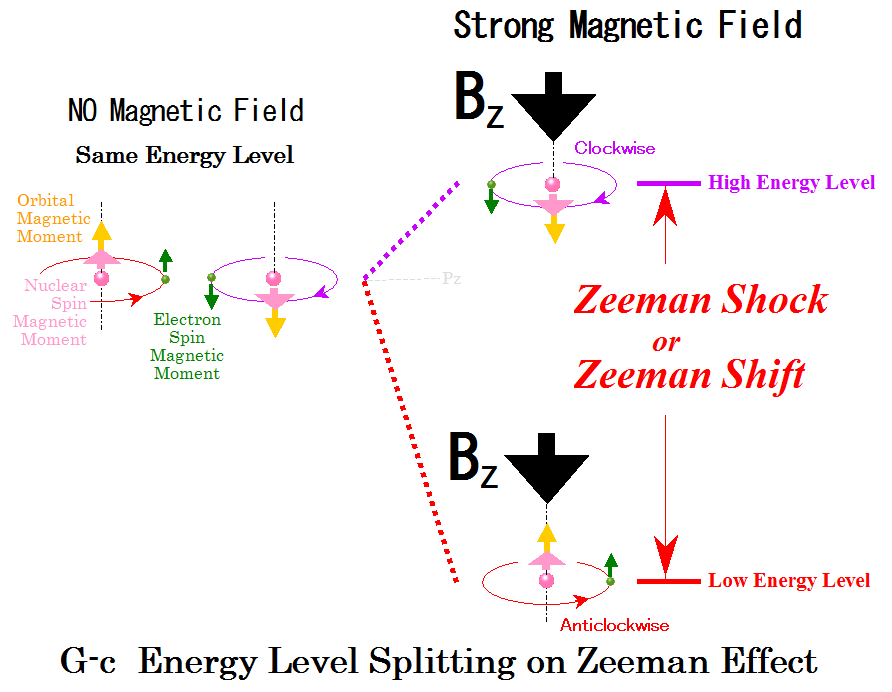
上図は、電子軌道・電子スピン・核スピンの3種類の磁気モーメントが同方向の場合だけですが、この場合が「Zeeman Shock」が最も大きくなります。
「エネルギー準位の分裂」は、原子スペクトルの「波長」で観測されます。
ゼーマン効果の偏光
ゼーマン効果では、原子スペクトルの「偏光」も同時に観測されます。「右らせん偏光」・「左らせん偏光」・「直線偏光」の特徴的なものです。
次図に示したように、この原子スペクトルの「偏光」は、「ローレンツ力」と「電子軌道の形状の変形」に由来します。
a) NO Magnetic Field
磁場が無い場合「p電子軌道の形状」は「楕円球状」です。
ランダムな方向を向いているため、「偏光」は「通常光」スペクトルです。各p軌道は、自身の軸方向へは光を発しません。
b) Weak Magnetic Field
外部磁場をZ軸方向のBzとします。電子軌道の反時計回り(赤)と時計回り(紫)の縮重が、磁場下の
「Lorentz Force」により解け、別のスペクトルとなります。
赤色の[Px or Py]は反時計回りの低エネルギー準位で高波長側に観測されます。「偏光」は「右らせん偏光」。
灰色の[Pz]は「(磁場と平行な)直線偏光」です。
しかしP軌道は自身の軸方向には発光しない為に、磁場Bz平行方向から観測すると確認できません。
磁場Bz垂直方向から観測すると「(磁場と平行な)直線偏光」が観測できます。
紫色の[Px or Py]は時計回りの高エネルギー準位で低波長側に観測されます。「偏光」は「左らせん偏光」。
微弱磁場下では、「電子軌道形状の変形」は、ほとんどありません。

c) Strong Magnetic Field
強磁場下では、G-c図に示したエネルギー準位の大分裂と、このG-d-1図で示す「p-電子軌道形状の著しい変形」が大問題です。
赤[Px or Py]軌道と
紫の[Px or Py]軌道の形状は、
共に極端にフラットなOblate spheroidに変形します。
このフラットに変形した形状に起因して、磁場Bzに垂直方向のスペクトルは、「(磁場に垂直な)直線偏光」に変わります。
磁場Bzに平行方向のスペクトルは、
赤[Px or Py]はAnticlockwise円偏光、
紫[Px or Py]はClockwise円偏光です。
同時にG-c図に示したように、赤と紫のエネルギー準位差もさらに著しく大きくなります。
灰色の[Pz]は、Opticalと重複しますが、ポール状に変形しProlate spheroidになります。磁場Bz垂直方向からのスペクトル観測により、「(磁場に平行な)直線偏光」が確認できます。これらは電子分布の変化、2次ゼーマン分裂にかかわっています。
これが1896年 P. Zeemanが発見したゼーマン効果です。この業績によりP. ZeemanとH. Lorentzは1902年にノーベル賞を受賞しています。
しかし100年以上たった今も、宙に浮いたまま、理論的に未確立の分野です。原因は、弱磁場下でのエネルギー準位差が非常に小さいため、「ピークの広がり」に丸め込まれスペクトルが正確に測定できず、確証が得られないためです。
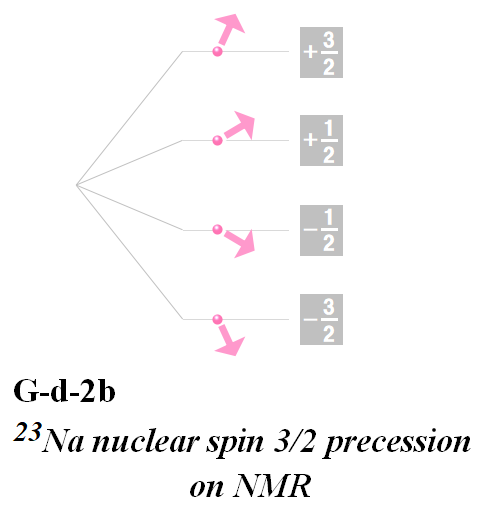
次図はNMRでの23Naの核スピン3/2の歳差運動です。Zeeman Effect のエネルギー準位とどのような整合性があるのかも研究中のようです。
次図は微弱磁場下のエネルギー準位のsplitと偏光スペクトルです。
最上位(mF=+3)と
最下位(mF=-3)のエネルギー準位は確定です。電子軌道は変形し偏光スペクトルとなり、エネルギー準位は大きくsplitします。Zeeman Shockです。しかししかし途中のエネルギー準位が最も重要です。これが無いとダメです。
"Just an idea" を示しました。Pz軌道と核スピンのcombinationに着目しました。
核スピン3/2は4個に分裂しています。

ゼーマン効果をもう少し見てみます。
次図左は、0.003Tの弱磁場下です。
Hyperfine Structureの2P1/2[F=2]は、2F+1=5個の (mF=+2,+1,0,-1,-2)へ分裂します。
Hyperfine Structureの2S1/2[F=1]は、2F+1=3個の(mF=-1,0,+1) へ分裂します。
この分裂が磁気副準位(1次ゼーマン)です。
磁場の有無による磁気副準位への分裂は、Combinationされた量子数により量子的です。
この磁気副準位(1次ゼーマン)の直近には、更に磁気副準位(2次ゼーマン)が存在し核スピン詳細も関連しているようですが検証中で図中には示していません。
同じ次図で、0.003T→0.03Tへ連続的に磁場強度を変化させます。
この連続的な磁場強度変化に対して、0.003Tでの各エネルギー準位(mF=+2,+1,0,-1,-2)は、それぞれ連続的に変化します。
図中"just an idea"で示したように、0.003TでのCombinationを保持したまま、「Bzに対するp軌道の角度」「スピン角度」等が連続的に変化していることになります。
![強磁場ゼーマン効果による、「スペクトル偏光」と「外部磁場Bzに対するp-電子軌道角度」 Polarized Atomic Spectra vs. p-Orbital angle[Bz] on Zeeman Effect (P1/2)](img-g/g21d-3b.gif)
この0.003Tで現れる量子化されたCombination(1次ゼーマン)、さらに0.03Tへと連続的に磁場強度を変化させた時にも保持されるCombinationを少し考察してみます。
「Bzに対するp軌道の角度」が、垂直な場合が紫と赤のσ[Px,Py]であり、平行な場合が中ほどのπ[Pz]であるとすると、「偏光」とも整合します。
これを円偏光の楕円率で見てみます。0.003Tの一番下。左から左らせん円偏光 → 左らせん楕円偏光 → 直線偏光 → 右らせん楕円偏光 → 右らせん円偏光と予想されます。しかし、まだ検証されていません。
更に、このモデルでは0.003Tのπ[Pz]軌道の準位(黄緑枠)に、⊿mF=-1(σ+), ⊿mF=0(π), ⊿mF=1(σ-)の3種類の遷移が同時に存在することになり、量子計算上、革新的です。
この場合の(π)は、「同じ核スピン状態間」の高遷移確率の電子遷移、つまり高輝度スペクトルです。
通常目視でも観測される炎色反応は、「同じ核スピン状態間」で、電子1個だけがp軌道状態→s軌道状態へ高遷移確率で変化し、この状態間のエネルギー準位差の発光hνです。
一方、両側の(σ+)と(σ-)は、低遷移確率(暗く目視で観測できない)ですが、「異なる核スピン状態間」の電子遷移です。
従来「電子遷移では核スピン状態は変わらない」とする通説でしたので、この意味でも革新的なモデルです。
電子遷移ですから「電子の状態(軌道・スピン)」は必ず変化しますが、同時に「核スピン状態」も変化しています。
つまり遷移確率は低いながら「電子の状態」と「核スピン状態」が同時に変化する電子遷移もあるということです。
この別経路らしきものが量子計算の実用化レベルまで達するのか、それとも多々あるモデルのノイズ音で終わらせるか、現在検証中です。
※ 1T(テスラ)は10,000gaussです。地磁気は0.5gauss程です。
ゼーマン効果の最後に、下図で、微細構造・超微細構造・ゼーマン効果のエネルギー準位を示しました。
100年以上前、P. Zeemanは太線で示した高遷移確率の輝線スペクトルを観測したと思われます。0.1~0.3T程度の磁場で測定したようです。これは現在でも再現されています。
図中の三角印▼は「ローレンツ力」によるClockwiseの高エネルギー化(紫)が無く、一様に低エネルギー化だけです。
完全に反対方向をむいている核スピンの影響が優勢のようです。
ただし次図のImageでは、
ParalleBz (Longitudinal)と
VerticalBz (Transverse)
が混在していますが、ParalleBzだけのエネルギー準位をもとにしています。VerticalBzのエネルギー準位を別に追加すると少し異なるImageになるかもしれません。しかしParalleBzと同じく、磁場強度の連続的な変化に対して、微弱磁場下で現れた軌道-電子スピン-核スピンの量子化されたCombinationが保持されたまま連続的に変化しそうです。

※ ファラデー効果
ゼーマン効果(Zeeman Effect)の偏光に似た現象として、ファラデー効果(Faraday Effect)があります。次図です。磁場に平行な直線偏光の光が、左旋性または右旋性の楕円偏光へ変化します。ただ異なる点は、左旋と右旋の楕円偏光の周波数は同じです。この点がゼーマン効果とは異なります。

ゼーマン効果は、更に磁場強度を強くしていくと、2Tまでは電磁石(またはネオジム磁石)ですが、更に強い5T及び7Tの超伝導磁石では、エネルギー準位の分裂は更に著しくなります。
*超伝導磁石は液体ヘリウム冷却(-269℃)です。この液体ヘリウムを、更に外側から液体窒素(-196℃)で2次冷却します。外側の液体窒素は少しづつ蒸発します。故に5T超の磁場では液体窒素の数日毎の補給・整備が必要です。
ただ研究薄膜ながらNdFeNx永久磁石は8テスラです。
実用化されると、「最強テスラNdFeBネオジム磁石」破りの「新超最強テスラNdFeNx磁石」となりそうで開発経過が注目されています。
実用化されれば液体窒素の補給作業はありません。
最後は参考として、数種類の元素の
2P3/2
エネルギー準位の強磁場下でのsplitです。

原子スペクトルの「ピークの広がり」
実際のICP原子スペクトルのピークは次のようなものです。
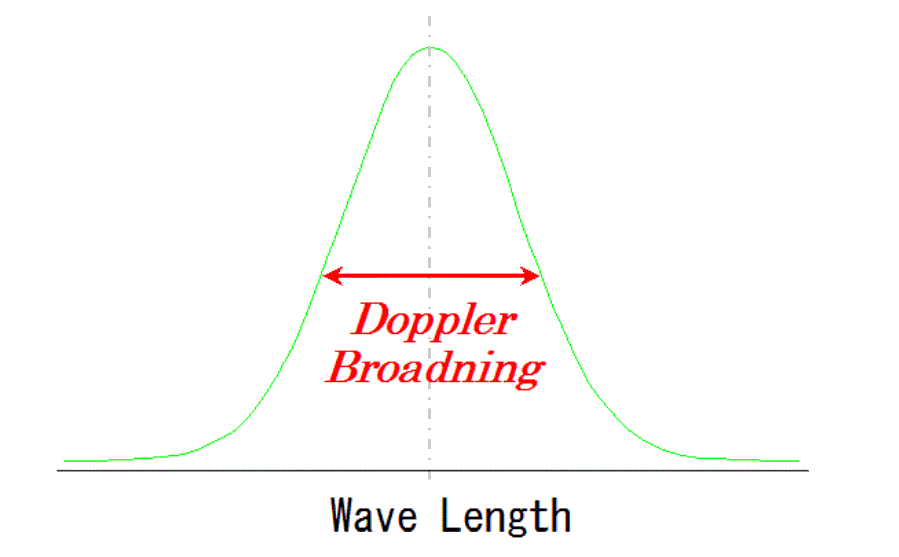
○ドプラー広がり
ICPによる原子スペクトルは、擬似炎で電子を励起し発光スペクトルを測定します。しかし質量m原子の速度vの大きさが、「ドプラー広がり」の原因となります。
光と音のドプラー効果は似ており次のような現象でした。
速度vで近づく場合は周波数が高くなり(高音へ)、速度vで遠ざかる場合は周波数が低くなる(低音へ)。
ICPの擬似炎中の質量m原子の速度vの大きさは相当なものです。
「近づく場合は低波長へ」と「遠ざかる場合は高波長へ」、2つは同じ確率であり、図のように左右対称の正規分布の広がりを持つスペクトルピークを示す。
この広がりの中に、超微細構造・弱磁場下Zeeman効果の大変小さなエネルギー準位差が、丸め込まれることになります。
○「不確定性原理」による広がり
陽子は電子の約1000倍の質量がありますが、約1.67×10-27[Kg]という軽さです。
当然「不確定原理」が当てはまります。m1+m2の重心が「不確定原理」により揺れるためスペクトルが広がります。
陽子だけでも「不確定原理」による揺れはあります。しかしドプラー広がりが支配的なICP原子スペクトルでは、これは小さく無視されます。
○2体問題における、X0Y0Z0座標の揺れに起因
陽子の動きに対して電子の動きは充分に速いと考えられます。
絶対座標XYZ座標の原点から見て、陽子はゆっくりとしか揺れず、まるで静止しているように見えます(不確定性原理の揺れもありますが)。
つまり絶対座標XYZ座標の原点から見て、陽子はまるで静止しているので、速い電子の動きに合わせてX0Y0Z0座標の原点(重心)を揺らさないといけないことになります。

重心をX0Y0Z0座標の原点にとって計算した計算値は、絶対座標に対して、X0Y0Z0座標の原点(重心)の揺れに伴う誤差を内包していることになります。しかし計算値自体はX0Y0Z0座標(球面座標)だけで重心を原点として次式で計算しているので、値は正確となります。
再掲
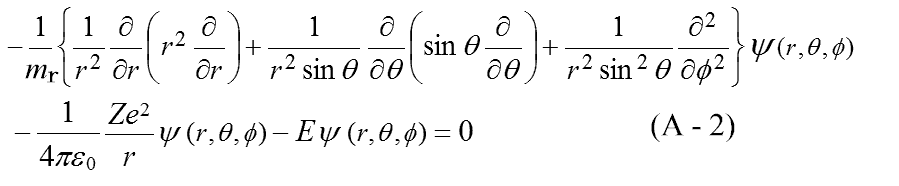
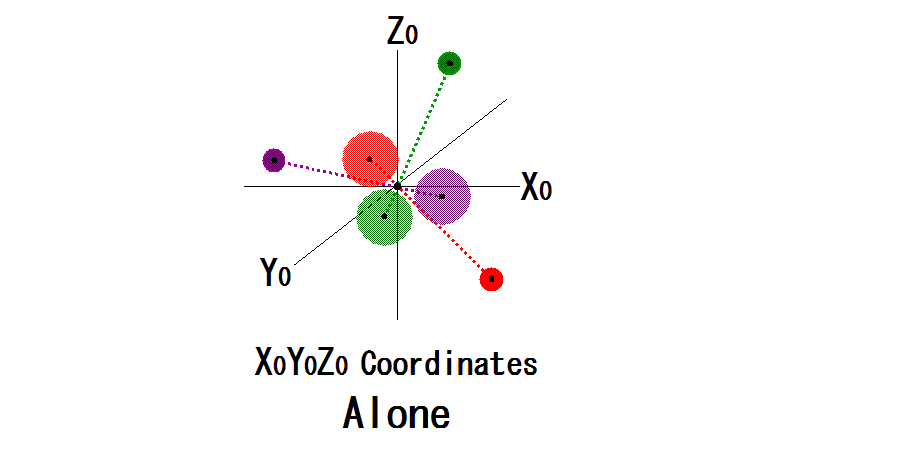
計算値に内包する誤差。波長シフトはありません。結局、スペクトル測定には関係ありません。
○他にも数種類ありますが、ドプラー広がりが支配的である。
並進運動
最後に「並進運動」です。前節で、原子スペクトル測定炎中の質量m原子の速度vの運動が、ドプラー広がりの原因であることが分かりました。これが「並進運動」です。
この測定炎中の原子の「並進運動」は、温度依存性のあるMaxwell-Boltzmann分布をなす速度vの気体分子の運動に、ほぼ相当すると考えられます。
A.2体問題
で、「電子軌道」と「並進運動」に分け、「電子軌道」の式(A-2) を解いてきました。
ここでは、もう一方の「並進運動」の式(A-1) を解きます。
再掲、式(A-1)

この方程式はポテンシャル項がないので座標変換せずに解きます。
m1+m2の重心の「並進運動」としていましたが、次のように簡略表示にします。

並進運動の関数Fと並進運動のエネルギーEtranslationalも次のように書き換えます。

式(A-1)は次のように書き換えられます。
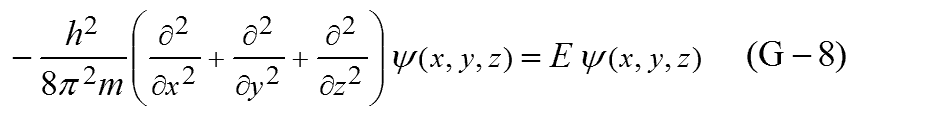
さらにx方向だけの運動しかないとして簡略化すると次のような式が得られます。
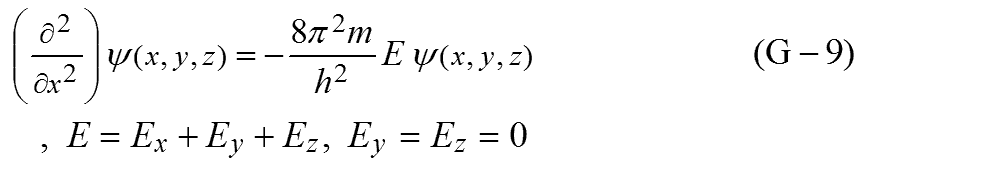
一方、Schrödingerの波動方程式でポテンシャル0の場で質量mの時間を考慮した式は次のようなものです。
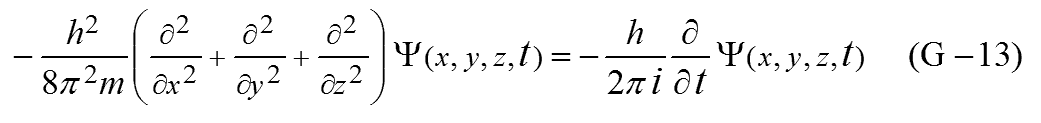
次のようにおき変数分離します。
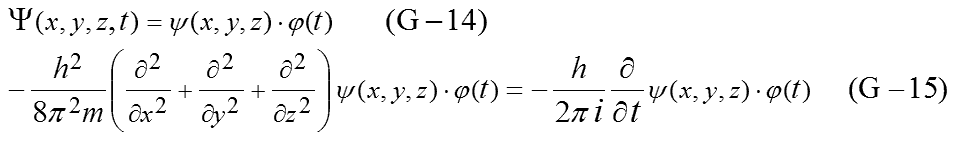
さらに整理していきます。

この式は左辺は変数x,y,zです。座標点(x,y,z)です。右辺は時間tです。この式は、「位置を決めれば時間は無限大になり、時間を決めれば位置が無限大になる」というHeisenbergの『不確定原理』を表しています。Heisenbergは行列式で解きましたが同じものとされています。
数学の一般で考えると、上式は左辺と右辺の変数が全く異なります。
この等式が常に成り立つためには両辺は同じ定数でなければなりません。
両辺をEとおくと次の2つの式に分離できます。

(G-17)を解くと次のようになります。

ここで、(G-15)をx方向だけの運動しかないとして簡略化すると次のようになります。
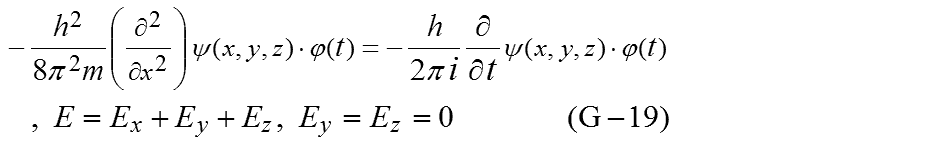
(G-18)を代入します。

右辺を整理していくと次のようになります。
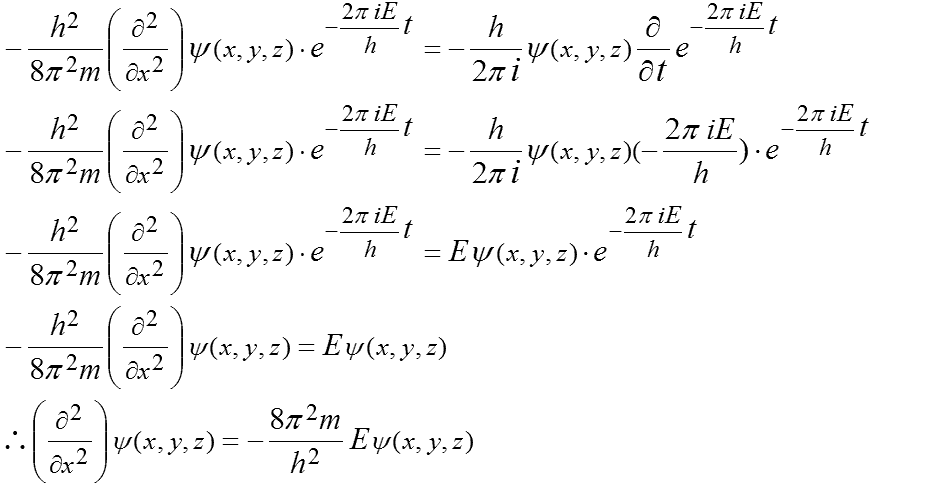
これは「並進運動」の式(G-9)と同じであり、一般的な定常状態の1次元の単振動の式でもあります。次のような解を持つことが分かっています。x0はサイン関数が0となる点です。Nは規格化定数です。

これを左辺に代入して整理すると次のようになります。
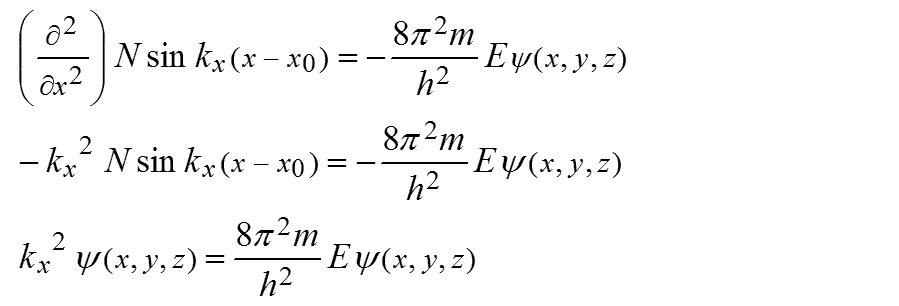
係数は等しいので次のようにkxが得られます。

一般的な定常状態の単振動ではk=2π/λであり、波長が次のように得られます。
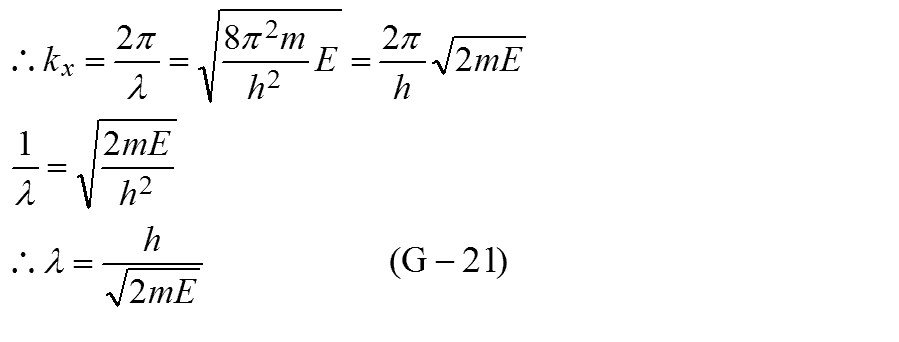
ポテンシャル0の場で質量mの時間を考慮した波動関数は次のように得られま

力学においては、質量mの粒子が速度vで動くと次のようなエネルギーとなります。

これを(G-21)に代入すると次のようなde Broglieの式が得られます。

つまり粒子でありながら、波動性を持つと言うことになります。
※ 2023 October 追記
2023年のノーベル物理学賞は、PhononのAttosecond physicsの研究チームが受賞しました。最先端の研究です。驚異的な極短時間パルスレーザーです。ファムト秒レーザーは30年前からありましたが、アト秒レーザーは一桁短いです。そして確かに電子軌道は位相の異なる3個の軌道が確認できます(例えばPx, Py, Pz電子軌道か)。少し話が跳びますが、これから「個々の変数x, y, zは、それぞれ独立であり、変数分離可能である。」という仮定が証明されたのではないでしょうか。
おわりに
今回は、重心を原点においた系で「電子と陽子の2質点運動エネルギー」と「静電ポテンシャルエネルギー」のみで、次のような「時間に依存しないシュレディンガーの波動方程式」をたて解いてきました。
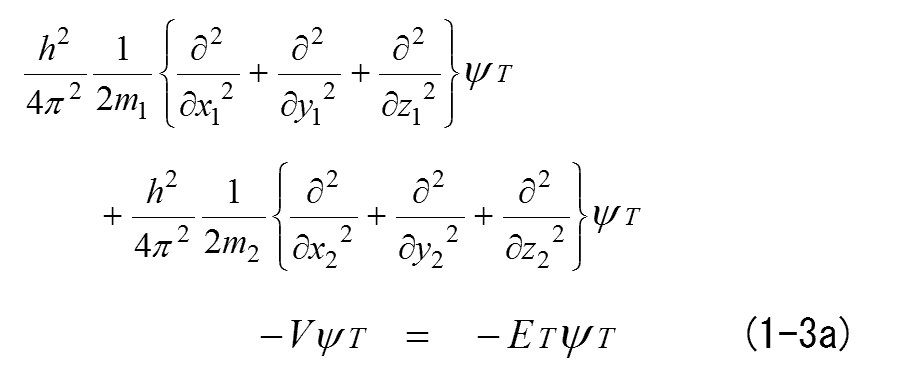
ここでVは静電ポテンシャルエネルギーです。
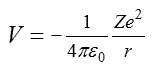
今回は「電子軌道」と「並進運動」は分離可能であるという前提で解きすすめてきました。しかし、既定路線としている前提条件が成り立たない場合、つまり個々に分離できない場合、もう1つの意見として、厳しい問題になります。
ここでは分離可能であると仮定して、「並進運動」を分離した「電子軌道」だけ、つまり重心が原点に固定された、以下の式(A-2)を解いてきました。
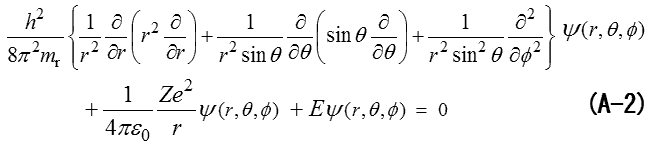
ここでラプラシアンを次のようにおき、

静電ポテンシャルエネルギー、
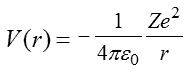
換算質量(reduced mass) mr、
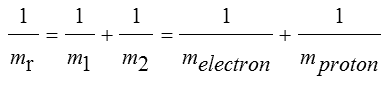
さらに次のようにおけば、
式(A-2)は次のように表せます。
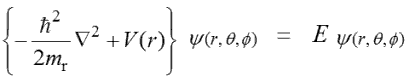
「運動エネルギー項」と「静電ポテンシャルエネルギー項」だけのハミルトニアンH0は次のように表せます。
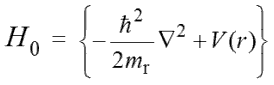
つまり今回は、水素原子における、以下の式を直接解いてきたことになります。
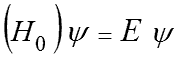
無磁場下の微細構造
「G-a Fine Structure・・」図で示した微細構造(fine structure)は、「電子軌道と電子スピンの相互作用」に起因するエネルギー準位の分裂です。ハミルトニアンHfsは次のように表せます。
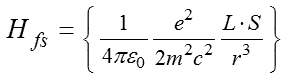
計算は次式を解くことになるのですが、直接には解けないので、「摂動法」により解きます。
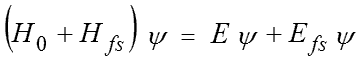
この式のハミルトニアンは以下のようになります。
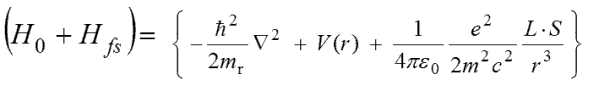
微細構造は、ほぼ全容がわかっているため成書が多くあり、ここでは述べません。
「G-b Energy Level of ・・」図で示した超微細構造および弱磁場下Zeeman効果は、原子スペクトルが正確に測定できないため、ハミルトニアンはまだ確定していません。
無磁場下の超微細構造
超微細構造(hyperfine structure)は、「核スピンとの相互作用」に起因するエネルギー準位の分裂です。ハミルトニアンHhfsは次のものです。計算は「摂動法」で解きます。式中のAは磁気双極子定数です。BとCは「原子核の形状の変形」に起因し、それぞれ核電荷4極子と核磁気8極子定数です。しかし、ほぼ全容がわかっているFine Structureの電子スピン・電子軌道に対して、核スピンを追加したHyperfine Structureのcombinationの全容は、まだ描けません。
微弱磁場下のZeeman効果
微弱磁場下のZeeman効果のハミルトニアンHweakBzは次のものです。計算は「摂動法」で解きます。
しかし無磁場下でのHyperfine Structureの核スピンのcombinationの全容が確定していないため、微弱磁場下で核スピンのcombinationの全容も、まだ描けません。

強磁場下のZeeman効果
微弱磁場下Zeeman効果とは著しく異なる様相を示します。 「激しいエネルギー準位分裂」と「軌道形状の著しい変形」が、強磁場下Zeeman効果では生じます。
これは
「G-c」図、
「G-d-1」図、
「G-d-3」図、
「G-d-3b」図、
「G-e」図、
「G-f」図
で示したように、「縮退がある」準位が強磁場下で激しく分裂します。
さらに1テスラ, 5テスラ, 10テスラへと磁場強度を強くすると、分裂はどんどん激しくなります。
ハミルトニアンをHstrongBzとすると、計算は次式を「摂動法」で解くことになります。

以上、今回は、電子スピン・核スピン・磁場を考慮しない、「運動エネルギー項」と「静電ポテンシャルエネルギー項」だけのハミルトニアンで、直接解きました。
ゆえに、いろいろと不具合はあるようです。しかし一方では、水素原子の「電子軌道」の3D構造・エネルギー準位などが得られ、初期量子力学の集大成とも言えるシュレディンガー方程式を、少しご理解いただけたと思います。
最後まで読んでいただいて、ありがとうございました。


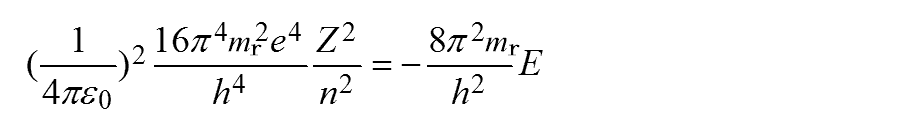
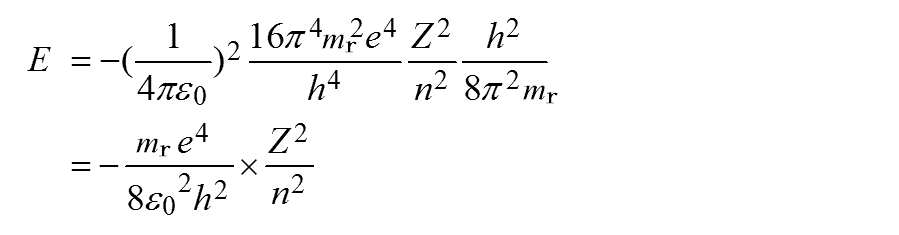
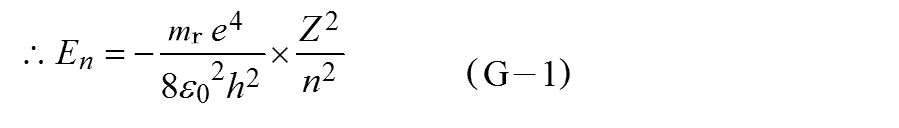

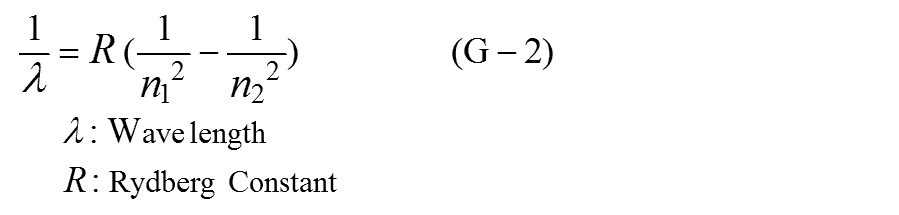


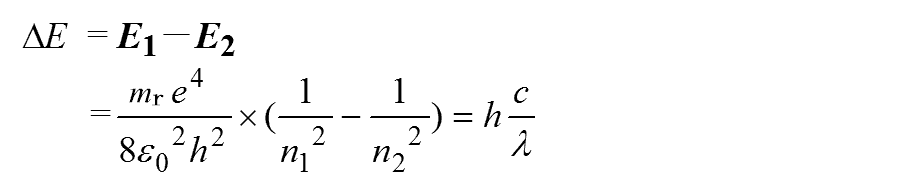
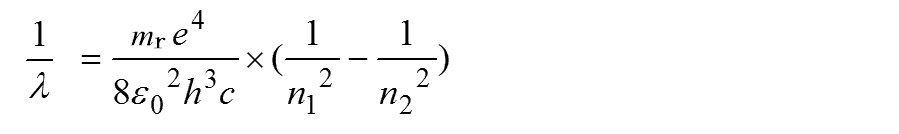


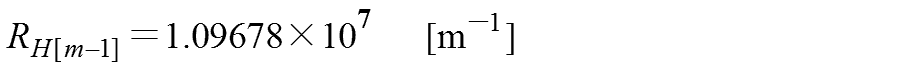
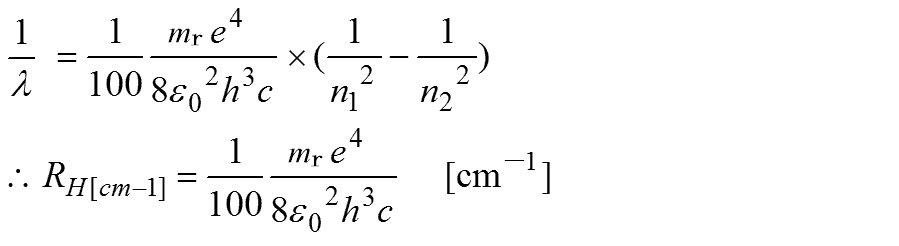











![強磁場ゼーマン効果による、「スペクトル偏光」と「外部磁場Bzに対するp-電子軌道角度」 Polarized Atomic Spectra vs. p-Orbital angle[Bz] on Zeeman Effect (P1/2)](img-g/g21d-3b.gif)